#Note #Computer-Graphics-and-Vision/Digital-Human

Parametric Human Models

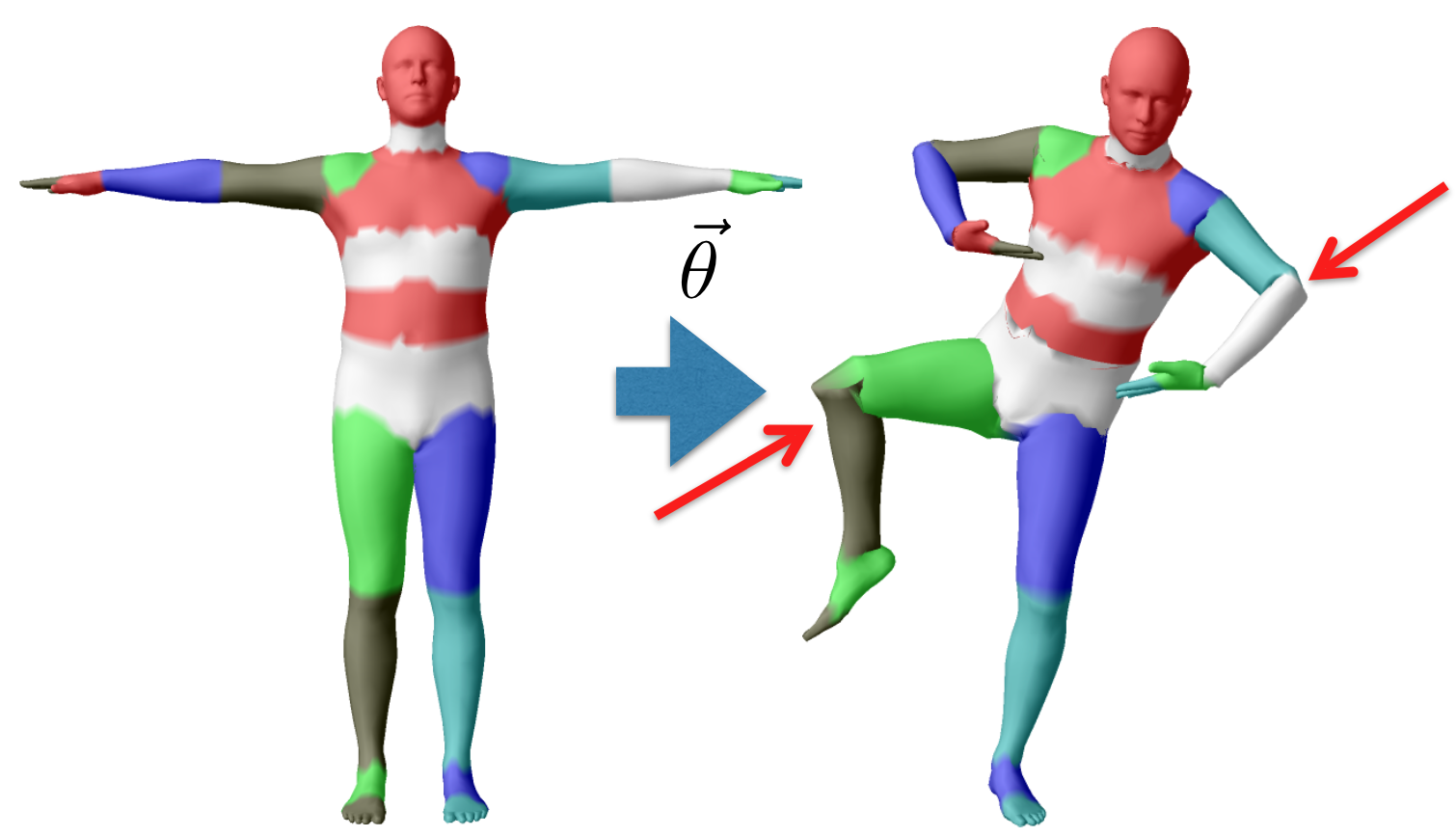
Pose Representation

Kinematic Chains

The human poses can be expressed via a kinematic chain, which is a series of local rigid body motions. The rotation of each joint can be represented by a vector $ω$ , whose norm is the angle of rotation, and direction is the axis of the rotation. Representing the relative coordinates of each joint with respect to its parent joint by $j$ , the transformation matrix form the local joint coordinates to the parent joint coordinates is

G (ω, j) = [\begin{matrix} e^{ω} & j \\ 0^{T} & 1 \end{matrix}] .

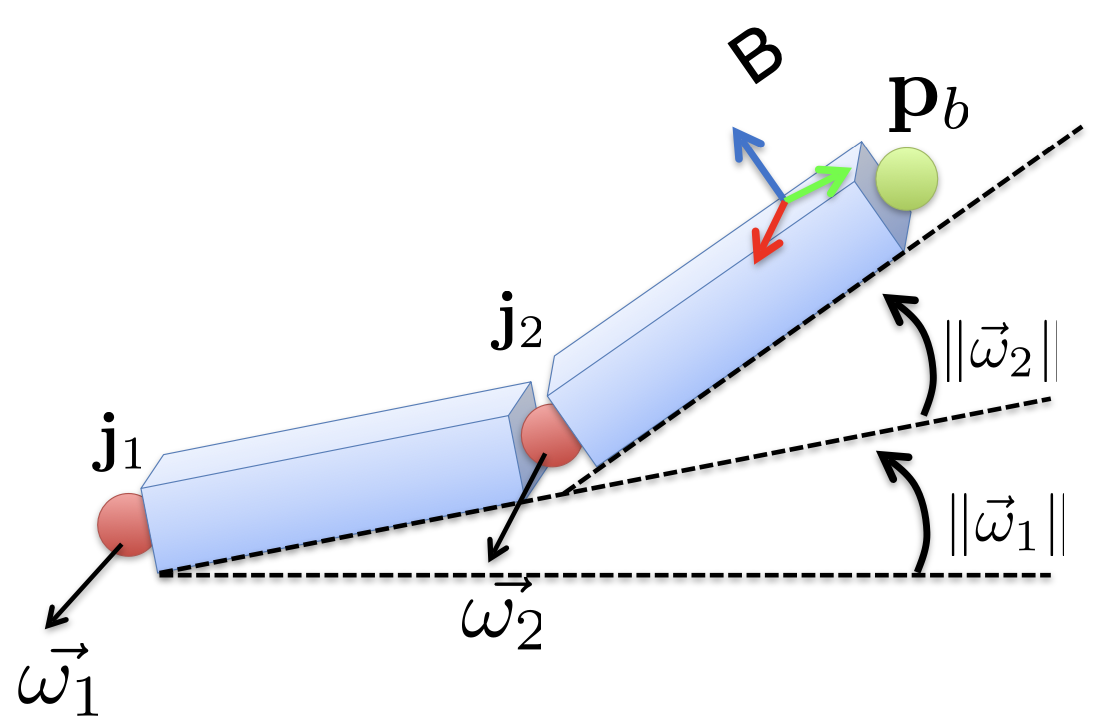
Pasted image 20240311165000.png|300
If we want to transform $p_{b}$ from coordinates of $j_{2}$ to world coordinates, we first represent $p_{b}$ is homogeneous coordinates ${\bar{p}}_{b} = {[\begin{matrix} p_{b} & 1 \end{matrix}]}^{T}$ , then
${\bar{p}}_{s} = G (ω_{1}, j_{1}) G (ω_{2}, j_{2}) {\bar{p}}_{b}$

Pose Parameters

If there are $K$ joints for a body model, we can represent the joint locations by a concatenated vector:

J = (\begin{matrix} j_{1} \\ ⋮ \\ j_{K} \end{matrix}) \in R^{3 K} .

The pose parameters, which are rotations of each joint, can be represented as a vector of concatenated axis-angles:

θ = (\begin{matrix} ω_{1} \\ ⋮ \\ ω_{K} \end{matrix}) \in R^{3 K} .

Problems of Kinematic Chains

Since points on the surface move along with the corresponding bones. If the transformations of two consecutive bones are different, there will be disconnectivity of surface points near joints.

Shape Representation

Linear Blend Skinning

In linear blend skinning (LBS), points are transformed as as blended linear combination of joint transformation matrices. For each vertex $t_{i}$ , we have a skinning weight assigned to it with respect to each joint $w_{k, i}$ . In homogeneous coordinates, the transformed position is

{\bar{t}}_{i}^{'} = \sum_{k = 1}^{K} w_{k, i} G_{k}^{'} (θ, J) {\bar{t}}_{i} .

Skinning Functions

Given $K$ joints and $N$ vertices, the standard skinning function produces transformed vertices from

Rest post vertices: $T \in R^{3 N}$ ,
Joint locations: $J \in R^{3 K}$ ,
Skinning weights: $W \in R^{N \times K}$ ,
Pose parameters: $θ \in R^{3 K}$ ,
which can be formulated as

T^{'} = W (T, J, W, θ) .

Problems of LBS

There are still artifacts when using LBS, especially when the joint angles are large
or when a bone undergoes a twisting motion. This will result in loss of volume.

Blend Shapes

Blend shapes are offsets added to vertex coordinates. The pose blend shapes, aimed to correct LBS issues, are a function of pose parameters. The shape blend shapes, aimed to introduce shape identity to each character, are fixed under all pose parameters.

The pose blend shape under the pose parameters $θ$ is calculated by multiplying the vectorized joint rotation matrices $f (θ) \in R^{9 K}$ by a pose blend shape matrix $P \in R^{9 K \times 3 N}$ :

B_{P} (θ) = f (θ) P .

The shape blend shapes are obtained by performing PCA on rest pose vertices of different characters. They are chosen to be the eigenvectors corresponding to the largest eigenvalues. Suppose we have $R$ shape blend shapes. The total shape blend shape can be calculated by

B_{S} (β) = \sum_{j}^{R} β_{j} S_{j} .

SMPL

Joint Regressor

The joint locations $J$ can also be seen as a linear function of rest vertices $T$ , parameterized by a joint regressor matrix $J \in R^{3 K \times 3 N}$ :

J = J (T; J) = J T .

SMPL

Putting these together, we have the SMPL model:

M (θ, β; T, S, P, W, J),

where

$θ \in R^{3 K}$ are the input pose,
$β \in R^{R}$ are the input shape,
$T \in R^{3 N}$ are the rest vertices,
$S \in R^{3 N \times R}$ are the shape blend shapes,
$P \in R^{9 K \times 3 N}$ are the pose blend shapes,
$W \in R^{N \times K}$ are the skinning weights,
$J \in R^{3 N \times 3 K}$ is the joint regressor.

Learning

Model Objective

In the Multishape database, there are about 2,000 single-pose registrations per gender. If we use this to train the model, we want to find the model parameters that minimize a single objective measuring the distance between model and registrations:

Φ^{*} = \underset{Φ}{argmin} \sum_{j} min_{θ_{j}, β_{j}} ‖ M (θ_{j}, β_{j}; Φ) - V_{j} ‖^{2},

where $Φ = {T, S, P, W, J}$ are the parameters to be learned, and $V_{j}$ are set of registrations.

Registration

In practice, we do not have registrations, which contain fixed number of vertices. We only have scanned point clouds ${S_{i}}$ . So we need to fit registrations to the raw scanned, and also need to fit the model to the registrations:

graph LR
    A[Data] --> B[Registration]
    B -- " " --> C[Model]
    C[Model] -- " " --> B

In the registration step, we aim to find a registration $V_{j}$ which minimizes the distance between scanned points $S_{j}$ and the registration surface $V (V)$ :

V_{j} = \underset{V}{argmin} \sum_{s_{i} \in S_{j}} dist (s_{i}, V (V)) + E_{prior} (V),

where $E_{prior} (V)$ is the prior loss for registration. However, optimizing vertices directly may lead to unstable results.

On the other hand, we can optimize the input parameters to the trained model, such that the model also fits the scanned points:

θ_{j}, β_{j} = \underset{θ, β}{argmin} \sum_{s_{i} \in S_{j}} dist (s_{i}, M (θ, β)) + E_{prior} (θ, β) .

However, we do not learn anything new from the scan. We just find the shape and pose parameters that can fit well.

Ultimately, we can combine these two objective together, to get the final objective

θ_{j}, β_{j}, V_{j} = \underset{θ, β, V}{argmin} \sum_{s_{i} \in S_{j}} dist (s_{i}, V (V)) + dist (V (V), M (θ, β)) + E_{prior} (θ, β),

which can be also formulated as follows:

V_{j} = \underset{V}{argmin} min_{θ, β} E_{reg} (S_{j}, V, θ, β),

where

E_{reg} (S_{j}, V, θ, β) = \underset{scan-to-mesh distance}{\underset{⏟}{E_{S} (S_{j}, V)}} + λ_{C} \underset{coupling}{\underset{⏟}{E_{C} (V, θ, β)}} + λ_{θ} \underset{pose prior}{\underset{⏟}{E_{θ} (θ)}} + λ_{β} \underset{shape prior}{\underset{⏟}{E_{β} (β)}} .

Scan-to-mesh Distance

The scan-to-mesh distance is calculated using the following:

E_{S} (S_{j}, V) = \sum_{s \in S_{j}} ρ (min_{v \in V (V)} ‖ s - v ‖),

where

ρ (x) = \frac{x^{2}}{σ^{2} + x^{2}}

is a robust function with upper bound.

Coupling

The coupling loss is defined as follows

E_{C} (V, θ, β) = {\begin{cases} ‖ V - M (θ, β) ‖_{F}^{2}, & if coupling on vertices, \\ ‖ A V - A M (θ, β) ‖_{F}^{2}, & if coupling on edges . \end{cases}

Priors

The priors are based on Mahalanobis distance if we assume a Gaussian distribution for both $θ$ and $β$ :

\begin{aligned} E_{θ} (θ) & = (θ - μ_{θ})^{T} Σ_{θ}^{- 1} (θ - μ_{θ}), \\ E_{β} (β) & = (β - μ_{β})^{T} Σ_{β}^{- 1} (β - μ_{β}) . \end{aligned}

Coregistration

From #Model Objective, we can train a model given registrations, and from #Registration, we can obtain registrations from trained models. To solve both problems at once, the key idea is to minimize the registration objective across the dataset of scans:

E ({S_{j}}, {V_{j}}, {θ_{j}}, Φ) = \sum_{j} (E_{S} (S_{j}, V_{j}) + λ_{C} E_{C} (V_{j}, θ_{j}, Φ) + λ_{θ} E_{θ} (θ_{j})) + \underset{model regularization}{\underset{⏟}{λ_{Φ} E_{Φ} (Φ)}} .

In training, the optimization of $Φ$ and ${V_{j}}$ are done alternatively, i.e., training one with the other fixed.