Variational Autoencoders

Autoencoders

• An autoencoder consists of an encoder $f$ and a decoder $g$.
• The encoder maps the original input from the input space $X$ to the latent space $Z$.
• The decoder reconstructs the sample from the latent space $Z$ to the input space $X$.
• Ideally, $f\circ g=\text{Identity}()$.

Formulation

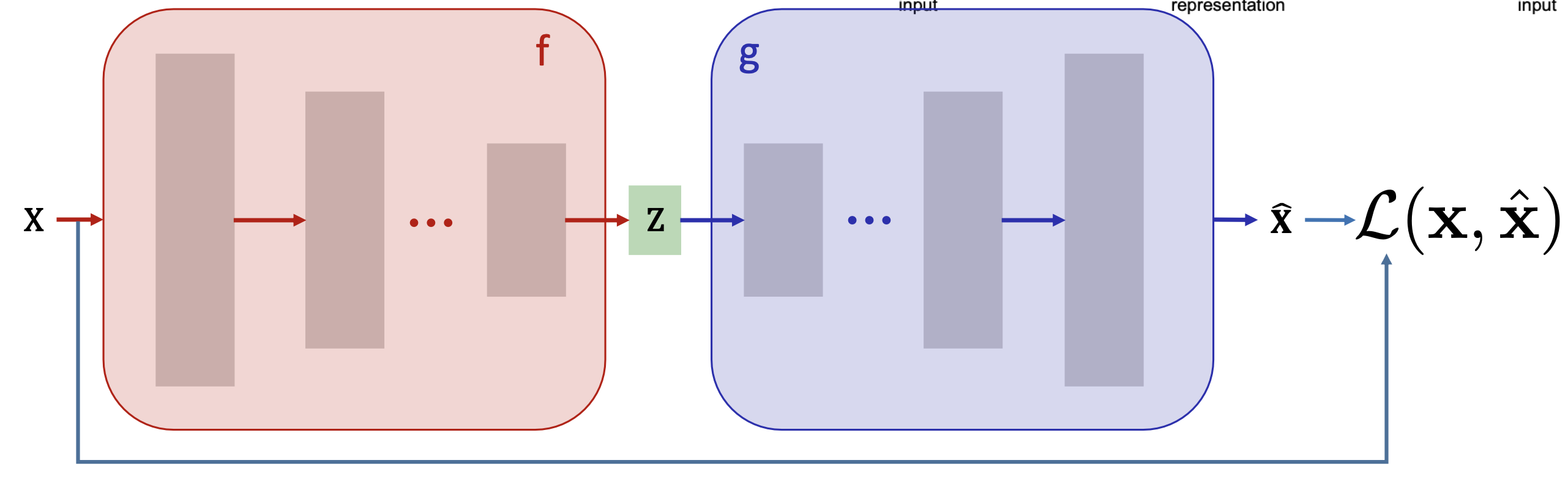
• Given two parameterized mappings $f(\cdot ;{\theta }_f)$ and $g(\cdot ;{\theta }_g)$, training consists of minimizing the reconstruction loss

• In linear cases, PCA is the optimal autoencoder that minimizes the reconstruction loss.

Dimensionality of Hidden Layer

• If $\text{dim}(\mathbf{z})<\text{dim}(\mathbf{x})$, the hidden layer is called undercomplete.
  • The hidden layer compresses the input.
  • Will compress well for training samples.
  • Hidden units will
    • Provide good features for training samples.
    • Bad for out-of-distribution samples.
• If $\text{dim}(\mathbf{z})>\text{dim}(\mathbf{x})$, the hidden layer is called overcomplete.
  • No compression.
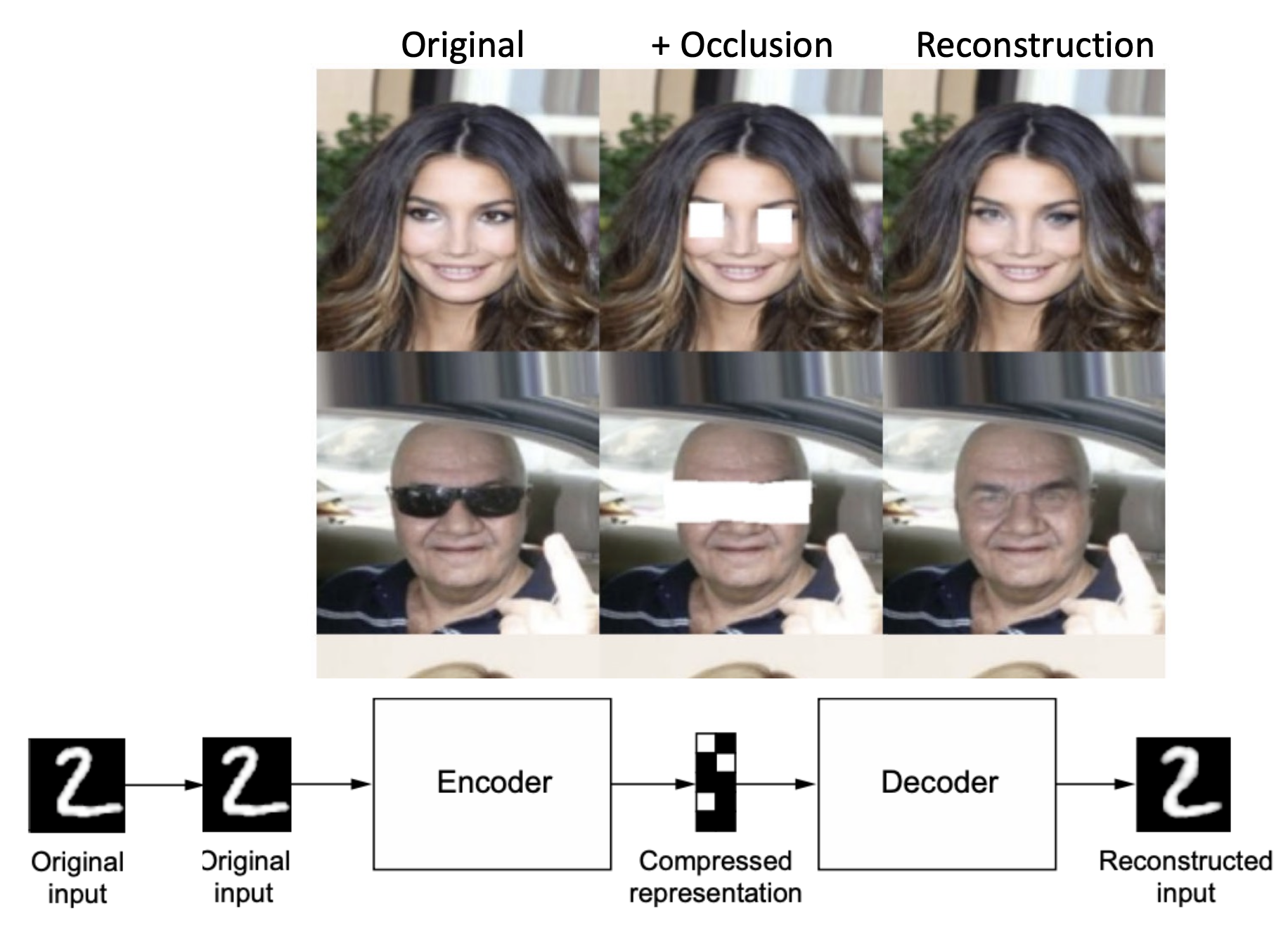
  • But should be robust to noise: also called denoising autoencoders.
  • Idea for training:
    1. Add some noise to the input $\mathbf{x}$ to get corrupted input $\tilde{\mathbf{x}}$.
    2. Reconstruction $\hat{\mathbf{x}}$ computed from $\tilde{\mathbf{x}}$.
    3. Loss compares $\hat{\mathbf{x}}$ with origin $\mathbf{x}$.

Limitations of Autoencoders

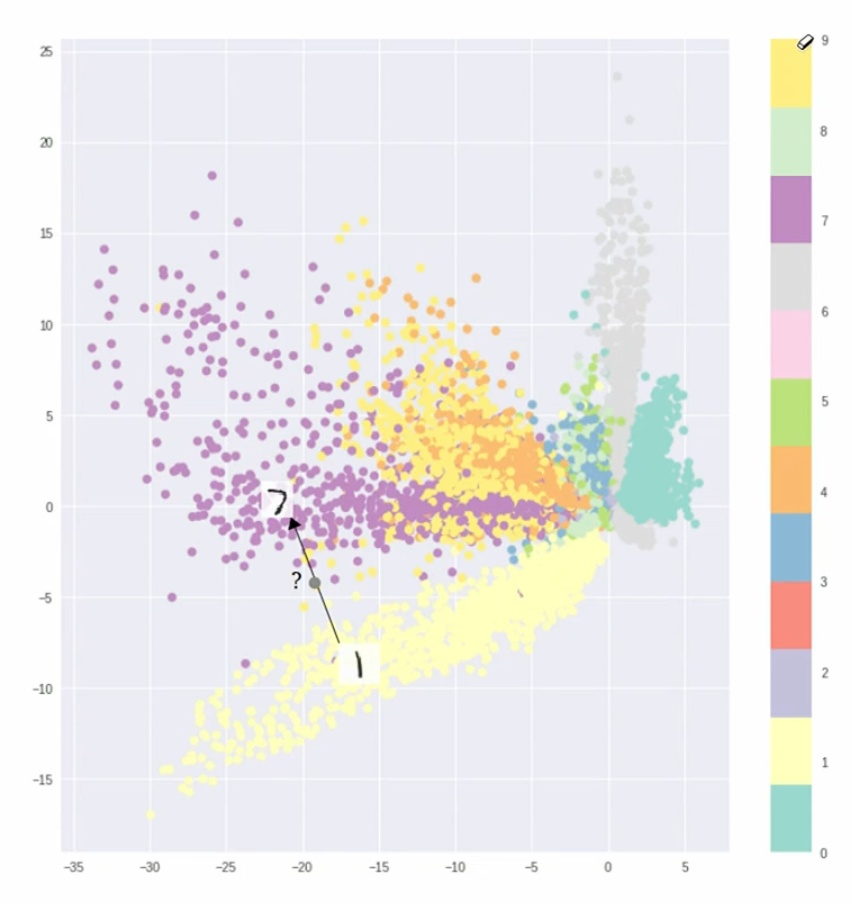
• The decoder is not able to generate good quality samples.
• The latent space is not well-structured: there are some places with no training samples.
  

Variational Autoencoders (VAE)

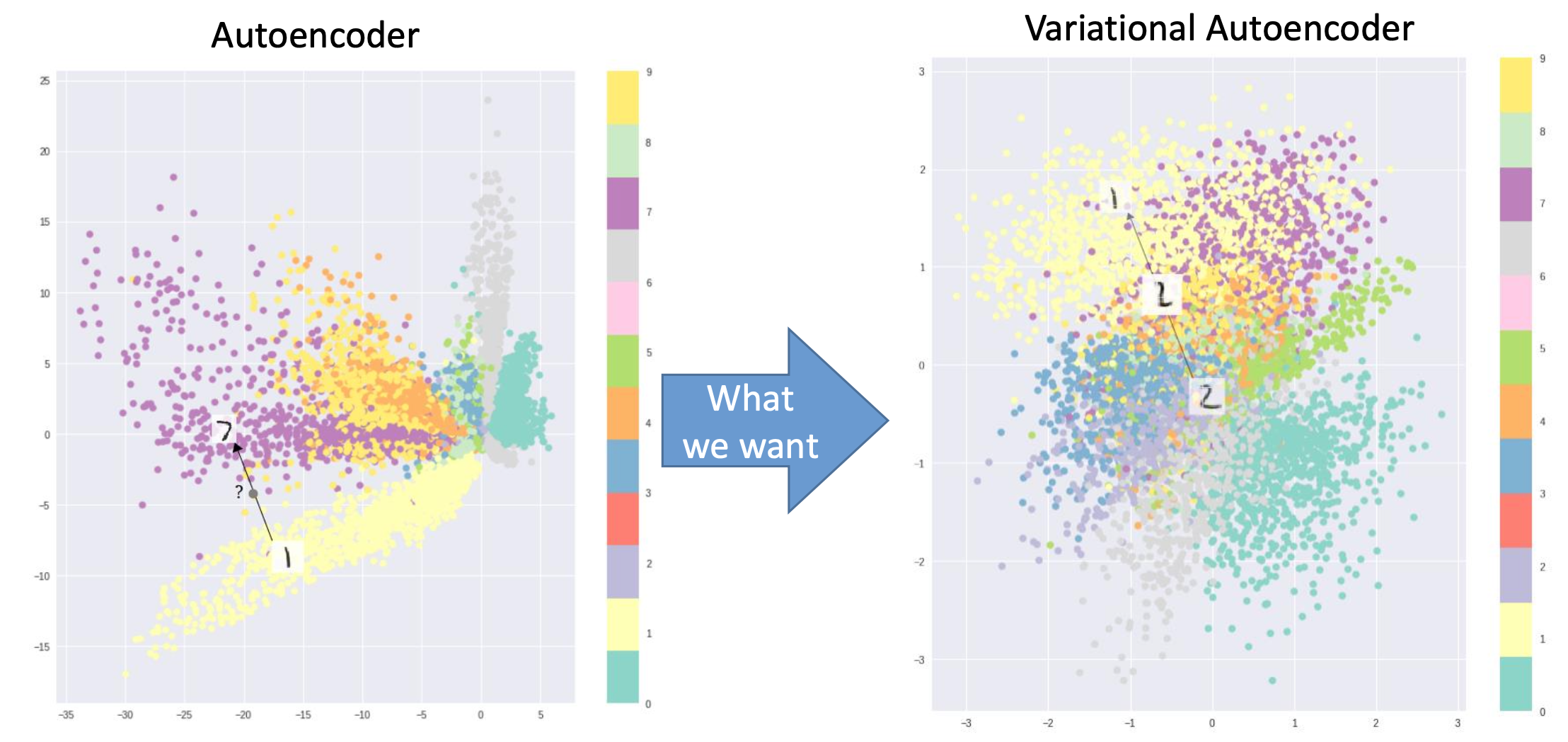
• Instead of predicting a single point in the latent space, we predict a Gaussian distribution

• We can generate new samples from the distribution.
• There is no "holes" in the latent space:

Modeling

• Assume the training data $\mathcal{D}=\{{\mathbf{x}}^{(i)}{\}}_{i=1}^N$ is generated from underlying latent distribution $\mathbf{z}$.
  • We first sample ${\mathbf{z}}^{(i)}$ from the prior distribution $p_{{\theta }^{\ast }}(\mathbf{z})$.
  • Then we sample ${\mathbf{x}}^{(i)}$ from the conditional distribution $p_{{\theta }^{\ast }}(\mathbf{x}\mid {\mathbf{z}}^{(i)})$.
• To best represent prior and conditional:
  • We need the prior to be a simple distribution (e.g. Gaussian), so we can sample from it.
  • We need the conditional to be complex enough to generate outputs like images: we can represent with DNN.

Training

• In training, we would like to learn model parameters that maximize likelihood of the training data

• However, the integral is intractable because we cannot integral for every $\mathbf{z}$
• The posterior density is also intractable

• The solution is to define additional encoder network $q_{\varphi }(\mathbf{z}\mid \mathbf{x})$ to approximate $p_{\theta }(\mathbf{z}\mid \mathbf{x})$ which is tractable (e.g. $q$ can be a Gaussian).

Data Log-Likelihood

Since $p_{\theta }({\mathbf{x}}^{(i)})$ does not depend on $\mathbf{z}$, we can write the log-likelihood as an expectation

Using Bayes' rule

• The expectation term is the decoder network.
• The KL divergence term is between Gaussians for encoder and $\mathbf{z}$ prior, which has closed-form solution.
• $\mathcal{L}({\mathbf{x}}^{(i)},\theta ,\varphi )$ is called evidence lower bound (ELBO), is the tractable lower bound we can maximize

Forward Pass

• Given the input $\mathbf{x}$, the encoder network $q_{\varphi }(\mathbf{z}\mid \mathbf{x})$ gives us a distribution of $\mathbf{z}$ to sample from

• Given the latent variable $\mathbf{z}$, the decoder network $p_{\theta }(\mathbf{x}\mid \mathbf{z})$ gives us a distribution of $\mathbf{x}$ to sample from

• In practice, the decoder only predicts the mean value $\hat{\mathbf{x}}={\mathit{\mu }}_{\theta }(\mathbf{z})$.

Reparameterization Trick

In order to calculate the gradient regardless of the randomness of sampling. When sampling from the posterior distribution $q_{\varphi }(\mathbf{z}\mid \mathbf{x})$, we first sample a random variable $\mathit{ϵ}\sim \mathcal{N}(\mathbf{0},\mathbf{I})$, then

Given standard normal distribution with $\mathit{\mu }$ and $\mathit{\sigma }$

Here the randomness is no longer a function of $\mathit{\mu }$ or $\mathit{\sigma }$, we can take derivative w.r.t. $\mathit{\mu }$ and $\mathit{\sigma }$.

VAE Loss

The VAE loss is derived from the ELBO

• The first term is reconstruction loss:
  • Similar samples close to each other.
• The second term is latent code loss:
  • Ensure compactness and smooth interpolation.

Generating Data

• Only use decoder.
• Sample $\mathbf{z}$ from $\mathcal{N}(\mathbf{0},\mathbf{I})$.
• Then sample $\mathbf{x}$ from $\mathcal{N}({\mathit{\mu }}_{\theta }(\mathbf{z}),\mathbf{I})$.

Learning Useful Representations

• Goal: learn features that captures similarities and dissimilarities.

• Requirement: objective that defines notion of utility.

• For autoencoders, we usually have entangled representation, which are individual dimensions in latent code encode some unknown combination of features in the data.

• We would like to learn features that correspond to distinct factors of variation (e.g. digits and style).
  

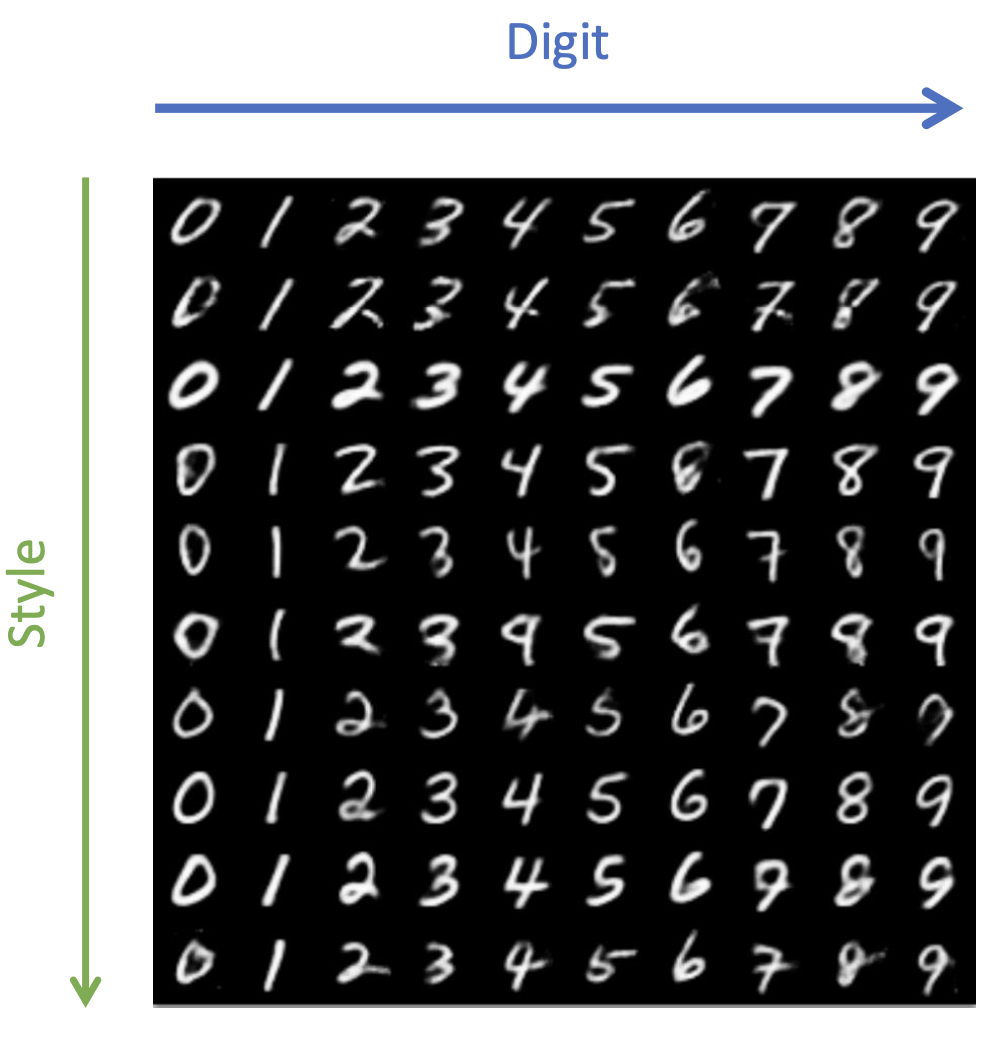
• Notion of utility: statistical independence can be used.

• Learning disentangled representation can be achieved with semi-supervised learning.

  • For example, we only learn style variable $\mathbf{z}$ with digit label $y$: $p_{\theta }(\mathbf{x}\mid \mathbf{z},y)$.
  • Here the style variable is conditionally independent from digit $y$.

$\beta$-VAE

• Goal: learn disentangled representation without supervision.
• Approach: modify the loss if the VAE by introducing an adjustable hyperparameter $\beta$ that balances latent channel capacity and independence constraints with reconstruction accuracy.
• Intuition: the KL loss enforces the distribution to be standard Gaussians, which is independent on each dimension; therefore, increasing the impact of KL loss can make the representation more disentangled.

We can also formulate it. Our goal is to maximize the reconstruction likelihood, while keeping the KL divergence lower than a threshold $\delta$:

Using Lagrange multiplier, we have the objective $\mathcal{F}(\theta ,\varphi ,\beta )$ to maximize

Therefore we have the weighted loss

Summary

• Intuition of VAE
  • Criteria of a good latent space
    • Meaningful degree of freedom (disentangled representations)
    • Continuity for interpolation
  • Autoencoders map each input to a point in the latent space, making the latent space full of holes and lack of continuity
  • Instead, we map the data to a smooth Gaussian distribution
• Theoretical background
  • Intractability of VAE
  • Optimizing the VAE by maximizing the ELBO: the derivation
• Encoder: Given input $\mathbf{x}$, predict the distribution of the latent variable $\mathbf{z}\sim \mathcal{N}({\mathit{\mu }}_{\varphi }(\mathbf{x}),{\sigma }_{\varphi }^2(\mathbf{x})\mathbf{I})$
• Reparameterization: Sampling $\mathbf{z}$ given the predicted distribution can be done by the following
  • Sample from the standard gaussian $\mathit{ϵ}\sim \mathcal{N}(\mathbf{0},\mathbf{I})$
  • Construct $\mathbf{z}$ as $\mathbf{z}={\mathit{\mu }}_{\varphi }(\mathbf{x})+{\sigma }_{\varphi }(\mathbf{x})\odot \mathit{ϵ}$
• Decoder: Given input $\mathbf{z}$, predict the distribution of the input $\mathbf{z}\sim \mathcal{N}({\mathit{\mu }}_{\theta }(\mathbf{x}),\mathbf{I})$
• Loss: the loss consists of reconstruction loss and KL loss
  • Reconstruction loss: MSE loss between the input $\mathbf{x}$ and the predicted mean of the decoder $\hat{\mathbf{x}}={\mathit{\mu }}_{\theta }(\mathbf{z})$
  • KL loss: the KL divergence between $q_{\varphi }(\mathbf{z}\mid \mathbf{x})=\mathcal{N}({\mathit{\mu }}_{\varphi }(\mathbf{x}),{\sigma }_{\varphi }^2(\mathbf{x})\mathbf{I})$ and the prior $p_{\theta }(\mathbf{z})=\mathcal{N}(\mathbf{0},\mathbf{I})$
• Generation:
  1. Sample $\mathbf{z}$ from $\mathcal{N}(\mathbf{0},\mathbf{I})$
  2. Use the decoder to sample from $\mathcal{N}({\mathit{\mu }}_{\theta }(\mathbf{x}),\mathbf{I})$
• $\beta$-VAE: multiplying the KL loss with a hyperparameter $\beta >1$ to make the model more disentangled